20171123 Notes: Application of Stochastic Structure Model: Control of Negative Reviews

This is the notes of Continuous Stochastic Structure Models with Apllication by Prof. Vijay S. Mookerjee. In this note, we are talking about an application of Stochastic Structure Model: Control of Negative Reviews.

Consider there is a firm $\mathcal{F}$ and on the website of this firm $\mathcal{F}$, customers can write their reviews and ratings on the website about this firm $\mathcal{F}$. What should the firm $\mathcal{F}$ do to suppress the negative effect of the negative reviews/ratings? How much effort should this firm make? What is the optimal strategy of response to the negative reviews/ratings?

Q1. Why do the responses to the negative reviews help?
A1. Customers need to browse the reviews and ratings to help them make their decision. There should be positive effect of responding to the negative reviews/ratings.
Q2. Must there be positive effect of replying to negative reviews?
A2. No. Some reviews might come from the irrational customers, thus replying to each negative reviews is not the optimal strategy. But there should be optimal strategy that could lead to positive effect.

Abstract Model

• State $X(t)$: Average of last $N$ most recent ratings
• 3 forces driving the state $X(t)$:
  • positive reviews
  • negative reviews
  • response to negative reviews

Arrival of reviews

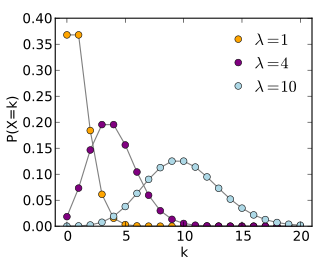
The arrival of reviews should follow Poisson Distribution $\mathcal{P}(\lambda)$

For instance, an individual keeping track of the amount of mail they receive each day may notice that they receive an average number of 4 letters per day. If receiving any particular piece of mail does not affect the arrival times of future pieces of mail, i.e., if pieces of mail from a wide range of sources arrive independently of one another, then a reasonable assumption is that the number of pieces of mail received in a day obeys a Poisson distribution.¹

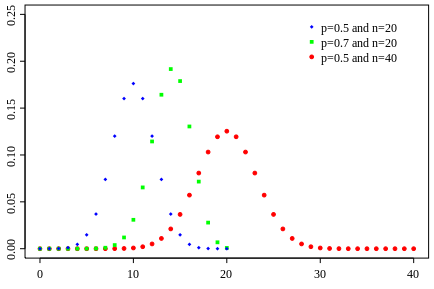
Comparison between Poisson Distribution and Binomial Distribution

• Poisson Distribution $\mathcal{P}(\lambda)$:
  • PMF: $\mathbb{P}(X=k) = \frac{e^{\lambda} \lambda^k}{k!}$, $ k \in {0,1,2,…}$
  • Expectation: $\lambda$
  • Variance: $\lambda$
  • MGF: $e^{\lambda(e^{t} - 1)}$

• Binomial Distribution $\mathcal{B}(n,p)$:
  • PMF: $\mathbb{P}(X=k) = \begin{pmatrix} n \\ k \end{pmatrix} p^k q^{n-k}$, $ k \in {0,1,2,…}$
  • Expectation: $np$
  • Variance: $npq$
  • MGF: $(q+pe^t)^n$

Recommended Reading: Neverland|20171104 Notes - Data Types

---

Table of Common Distributions - TAMU Stat

---

Deriving Poisson Distribution from Binomial Distribution

See the notes of Andrew Chamberlain, Ph.D. from the Medium Medium|Deriving the Poisson Distribution from the Binomial Distribution, which is quite clear. One helpful reminder is $\lim_{n \to \infty} (1+\frac{1}{n})^n = e$, where $e$ is the Euler’s number. And based on this definition, $\lim_{n \to \infty} (1-\frac{c}{n})^n = e^{-c}$.

Does subset of Poisson still follow Poisson Distribution?³:

$X = r$ follow Poisson Distribution $\mathcal{P}(\lambda)$, and select $Y = k$ with probability $p$ from $X$.

Question:Does $Y=k$ still follow Poisson Distribution? If so, what kind of Poisson Distribution?
Proof:

• Marginalization: $\mathbb{P} (Y=k) = \sum_{r=k}^{+\infty} \mathbb{P} (X=r,Y=k) = \sum_{r=k}^{+\infty} \mathbb{P} (X=r) \cdot \mathbb{P} (Y=k|X=r)$;
• $\mathbb{P} (X=r)$ should be PMF of Poisson Distribution $\mathcal{P}(\lambda)$ and $\mathbb{P} (Y=k|X=r)$ should be Binomial Distribution $\mathcal{B}(r,p)$; $$\mathbb{P} (Y=k) = \sum_{r=k}^{+\infty} \frac{e^{-\lambda} \lambda^r}{r!} \begin{pmatrix} r \\ k \end{pmatrix} p^k q^{r-k}$$ $$= \sum_{r=k}^{+\infty} \frac{e^{-\lambda} \lambda^r}{r!} \frac{r!}{(r-k)!(k)!} p^k q^{r-k}$$ $$= \frac{e^{-\lambda} p^k}{k!} \sum_{r=k}^{+\infty} \frac{\lambda^r q^{r-k}}{(r-k)!}$$ $$\stackrel{s=r-k}{=} \frac{e^{-\lambda} (\lambda p)^k}{k!} \sum_{s=0}^{+\infty} \frac{\lambda^s q^{s}}{(s)!}$$ $$= \frac{e^{-\lambda p} (\lambda p)^k}{k!} \sum_{s=0}^{+\infty} \frac{e^{-\lambda q} (\lambda q)^s}{(s)!}$$ $$= \frac{e^{-\lambda p} (\lambda p)^k}{k!}$$ which is MPF of Poisson Distribution $\mathcal{P}(\lambda p)$.

Modeling the state

$$dX(t) = (\rho \lambda (1-p)(b-X) - \beta \lambda \rho X + \alpha (b-X)) dt + \sigma sqrt{b-X}$$

• Force 1: Positive, $\rho \lambda (1-p)(b-X)$;
• Force 2: Negative, $\beta \lambda \rho X$;
• Force 3: Firm can control, $\alpha (b-X)$

$X_t$ is CIR process.

---

Recommended Reading: Neverland|20171117 Notes: Stochastic Process, Parameter Estimation, PDE

---

Data

$X_t$ state: Average of last n most recent ratings, e.g. $n = 20$.

Ctrip data of reviews and ratings from 2012.4 to 2014.6

DID Analysis: $\Delta r_j = \frac{1}{n} \sum_{i=j+1}^{j+n} r_i - \frac{1}{n} \sum_{i=j-n}^{j-1} r_i$, where $n$ is the window size.

Measure improvement of ratings from response, $\Delta r_j$ increase after response.
Average Similarity Scores using TF-IDF decrease after response.
Length of negative review increase after response, which means that the cost of writing negative review increase.

---

• Chi-Square test
• Information Gain Ratio
• Receiver operating characteristic (ROC Curve)

---

Propensity Score Matching (PSM):

$$Rating_{i,j,t}= \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \beta_3 \\ \end{bmatrix}^T \begin{bmatrix} 1 \\ Treatment_{i,j} \cdot Period_{i,j,t} \\ Treatment_{i,j} \\ Period_{i,j,t} \\ \end{bmatrix}+\delta_{j}+\epsilon_{i,j,t}$$

Validation of Poisson Distribution

Q-Q Plot

Parameter Estimation

$k_1, k_3, \sigma$ $\leftrightarrow$ $\alpha, \beta, \rho, p, \lambda, \sigma$

we don’t care about $sigma$.
$\lambda$: Review arrival rate;
$p$: Prob{Negative Review} $\rightarrow$ separate $\beta$ out

3 equations and 5 parameters to be estimated:

$$\left\{ \begin{aligned} k_1 = \alpha + \beta \lambda p + \rho \lambda (1-p) \\ k_3 = \frac{5 \beta \lambda p}{\alpha+\beta \lambda p + \rho \lambda (1-p)} \\ k_1 k_3 = 5 \beta \lambda p \end{aligned} \right.$$

Go outside of the problem and find data, separate “endogenous”:

• When no response, $\alpha=0$
• After response, $\alpha>0$

In equation of $k_1$, we can separate $\alpha$ and $p$

Prediction compared with ARIMA/GARCH

$ARIMA(p,q)$, $GARCH(p,q)$ $\stackrel{V.S.}{\Leftrightarrow}$ SDE

Probability Response Strategy:

• Mean control
• Mean-Variance Control
• Service-level Control

Recommended Reading: Baoduge|TIME SERIES ANALYSIS WITH ARIMA/GARCH MODEL

---

¹. Statistics|The Poisson Distribution ↩

³. CrossValidate|Is a subset of a Poisson process also following a Poisson process? ↩