Model and Data Source
Source: Linear Regression on house pricing on Kaggle posed by Aditya Sharma.
- $sqfr_{living}$ is square footage of the home;
- $bedrooms$ is Number of Bedrooms/House;
- $bathrooms$ is Number of bathrooms/bedrooms;
- $grade$ is overall grade given to the housing unit, based on King County grading system;
- $sqft_{above}$ is square footage of house apart from basement;
- $zipcode$ is zip code;
Here is Description of Data
Load Data
Here is our data:
1 | rm(list=ls()) |
## [1] 21613 21
1 | class(hprice) |
## [1] "data.frame"
1 | names(hprice) |
## [1] "id" "date" "price" "bedrooms"
## [5] "bathrooms" "sqft_living" "sqft_lot" "floors"
## [9] "waterfront" "view" "condition" "grade"
## [13] "sqft_above" "sqft_basement" "yr_built" "yr_renovated"
## [17] "zipcode" "lat" "long" "sqft_living15"
## [21] "sqft_lot15"
1 | # # obervations |
## [1] 21613
1 | # price in 100K |
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.750 3.220 4.500 5.401 6.450 77.000
1 | ## Writing multiple linear regression model without zipcode |
##
## Call:
## lm(formula = price ~ sqft_living + bedrooms + bathrooms + grade +
## sqft_above + zipcode, data = hprice)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.535 -1.307 -0.233 0.941 45.523
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.600e+02 3.179e+01 -17.619 < 2e-16 ***
## sqft_living 2.708e-03 4.541e-05 59.637 < 2e-16 ***
## bedrooms -3.870e-01 2.262e-02 -17.109 < 2e-16 ***
## bathrooms -2.160e-01 3.437e-02 -6.285 3.34e-10 ***
## grade 1.072e+00 2.364e-02 45.343 < 2e-16 ***
## sqft_above -6.577e-04 4.422e-05 -14.874 < 2e-16 ***
## zipcode 5.654e-03 3.240e-04 17.453 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.445 on 21606 degrees of freedom
## Multiple R-squared: 0.5564, Adjusted R-squared: 0.5563
## F-statistic: 4517 on 6 and 21606 DF, p-value: < 2.2e-16
1 | #========================== |
## [1] TRUE
1 | dim(X) |
## [1] 21613 7
1 | # True beta |
## [1] TRUE
1 | class(beta) |
## [1] "numeric"
1 | length(beta) |
## [1] 7
1 | # |
## [1] 3.671272
Monte Carlo Simulation
Next, we are running Monte Carlo Simulation.
One Replication Example
1 | set.seed(12345) |
## [1] "matrix"
1 | is.vector(Y) |
## [1] FALSE
1 | is.matrix(Y) |
## [1] TRUE
1 | length(Y) |
## [1] 21613
1 | ff<-lm(Y~X[,-1]) |
##
## Call:
## lm(formula = Y ~ X[, -1])
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.2654 -2.4292 -0.0042 2.4559 14.2330
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.265e+02 4.747e+01 -11.090 < 2e-16 ***
## X[, -1]1 2.764e-03 6.782e-05 40.757 < 2e-16 ***
## X[, -1]2 -3.943e-01 3.378e-02 -11.673 < 2e-16 ***
## X[, -1]3 -1.999e-01 5.134e-02 -3.893 9.91e-05 ***
## X[, -1]4 1.046e+00 3.531e-02 29.630 < 2e-16 ***
## X[, -1]5 -7.062e-04 6.604e-05 -10.693 < 2e-16 ***
## X[, -1]6 5.313e-03 4.838e-04 10.981 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.652 on 21606 degrees of freedom
## Multiple R-squared: 0.3593, Adjusted R-squared: 0.3591
## F-statistic: 2020 on 6 and 21606 DF, p-value: < 2.2e-16
1 | sum2 <- summary(ff2) |
##
## Call:
## lm(formula = Y ~ X[, c(-1, -3)])
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.9540 -2.4375 -0.0134 2.4516 14.5602
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.549e+02 4.756e+01 -11.668 < 2e-16 ***
## X[, c(-1, -3)]1 2.511e-03 6.446e-05 38.954 < 2e-16 ***
## X[, c(-1, -3)]2 -3.120e-01 5.059e-02 -6.168 7.05e-10 ***
## X[, c(-1, -3)]3 1.120e+00 3.485e-02 32.145 < 2e-16 ***
## X[, c(-1, -3)]4 -6.750e-04 6.619e-05 -10.197 < 2e-16 ***
## X[, c(-1, -3)]5 5.591e-03 4.848e-04 11.534 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.664 on 21607 degrees of freedom
## Multiple R-squared: 0.3553, Adjusted R-squared: 0.3551
## F-statistic: 2381 on 5 and 21607 DF, p-value: < 2.2e-16
1 | #============================== |
## 2.5 % 97.5 %
## (Intercept) -6.195125e+02 -4.334107e+02
## X[, -1]1 2.631084e-03 2.896935e-03
## X[, -1]2 -4.605151e-01 -3.280933e-01
## X[, -1]3 -3.005168e-01 -9.925815e-02
## X[, -1]4 9.770620e-01 1.115488e+00
## X[, -1]5 -8.356179e-04 -5.767387e-04
## X[, -1]6 4.364900e-03 6.261629e-03
1 | class(cfi) |
## [1] "matrix"
1 | dim(cfi) |
## [1] 7 2
1 | # If true beta is in confidence interval of estimated beta |
## [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE
1 | class(flag.beta) |
## [1] "logical"
1 | length(flag.beta) |
## [1] 7
1 | #============================== |
## [1] 13.33942
1 | #============================== |
## (Intercept) X[, -1]1 X[, -1]2 X[, -1]3 X[, -1]4
## -5.264616e+02 2.764009e-03 -3.943042e-01 -1.998875e-01 1.046275e+00
## X[, -1]5 X[, -1]6
## -7.061783e-04 5.313264e-03
1 | #============================== |
## (Intercept) X[, -1]1 X[, -1]2 X[, -1]3 X[, -1]4 X[, -1]5
## FALSE FALSE FALSE FALSE FALSE FALSE
## X[, -1]6
## FALSE
1 | class(flag.type1) |
## [1] "logical"
1 | length(flag.type1) |
## [1] 7
Running Monte Carlo Simulation
1 | # Vector of N (Replication number) |
Plot of N = 500
1 | # In Distribution pic, bulue line is true beta, red line is betahat |
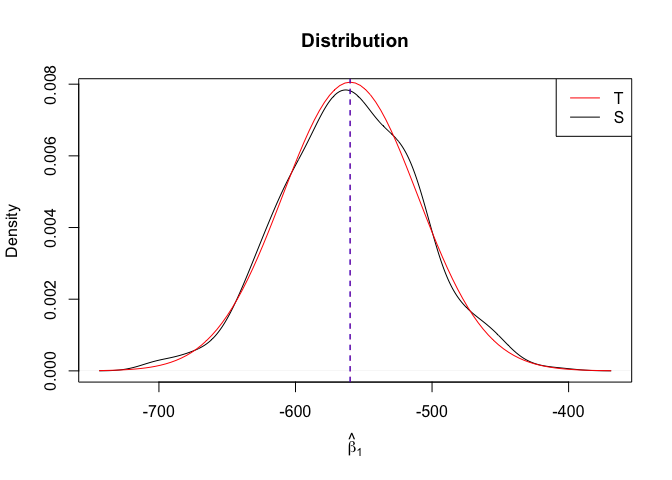
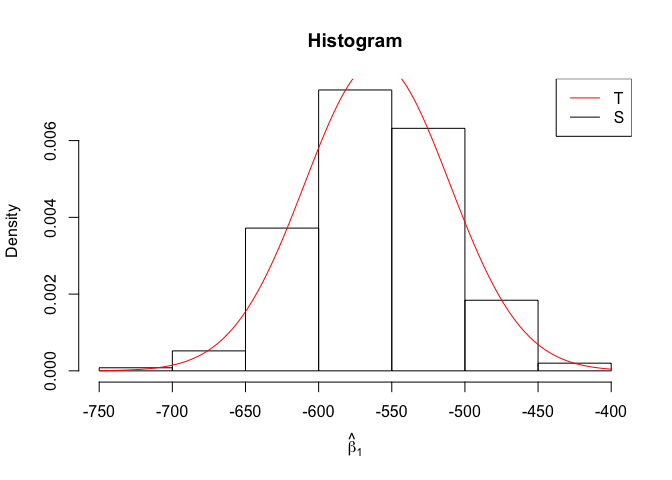
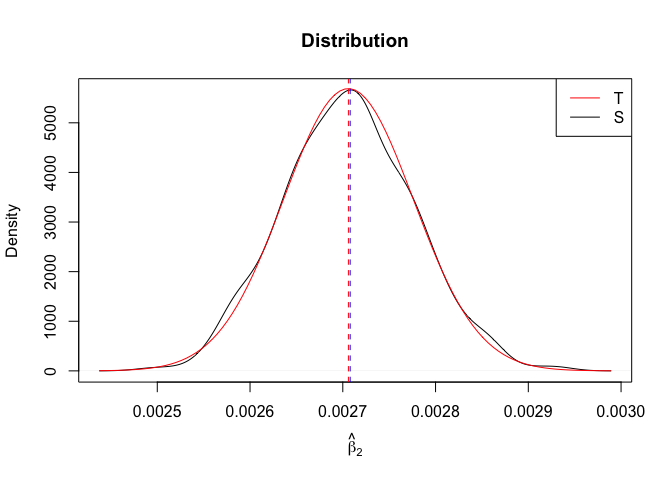
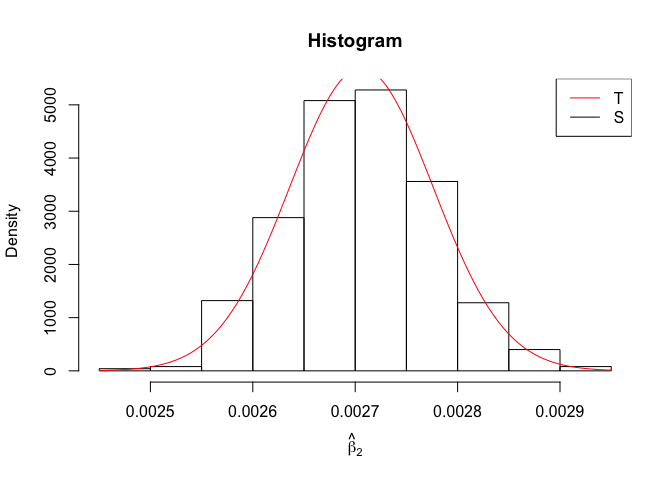
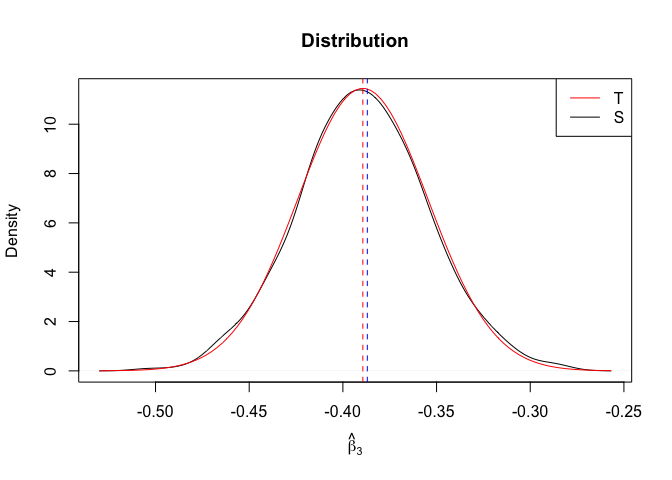

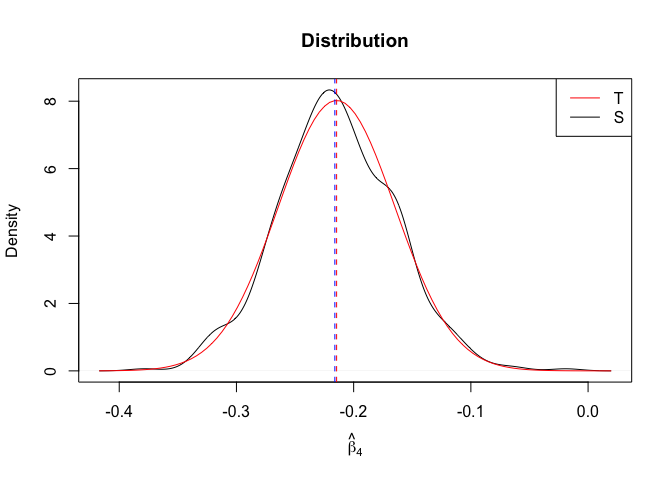
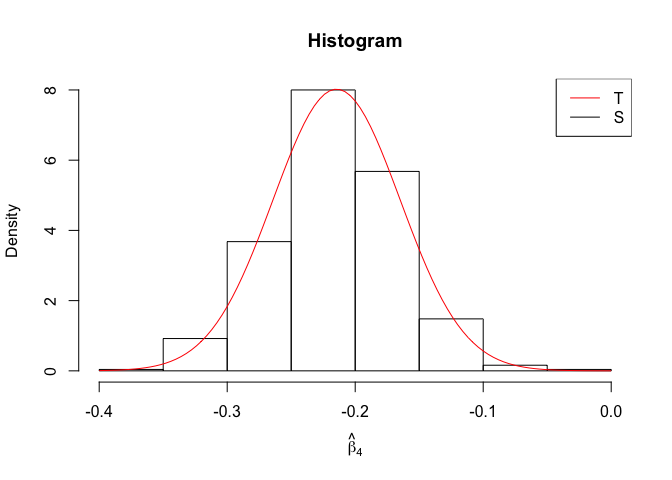
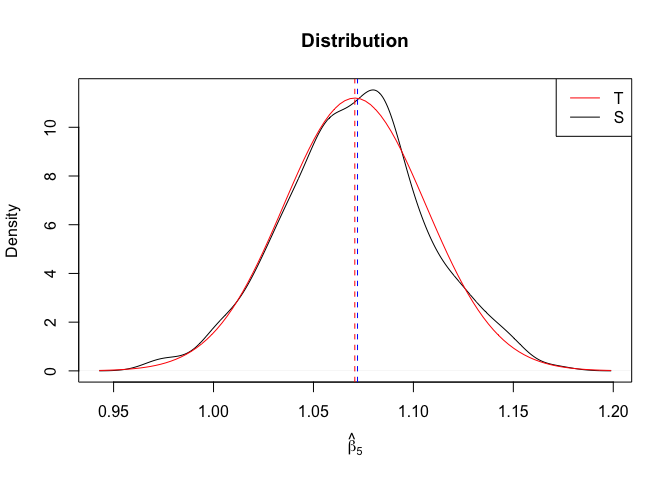
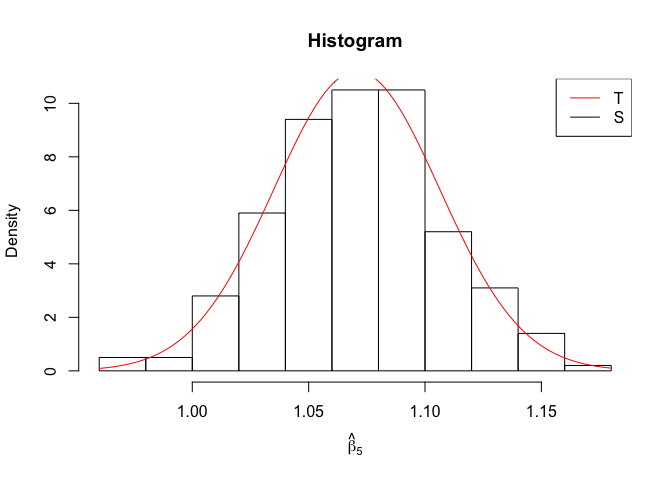
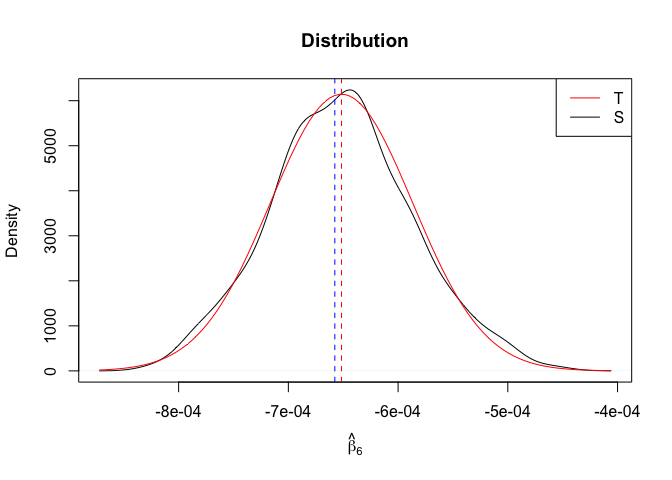
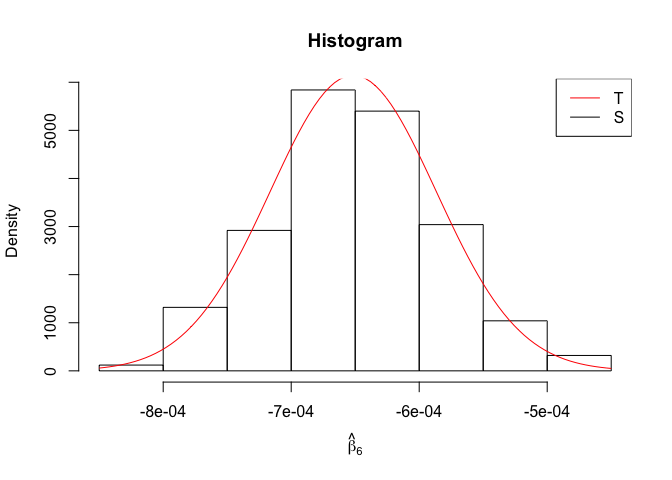
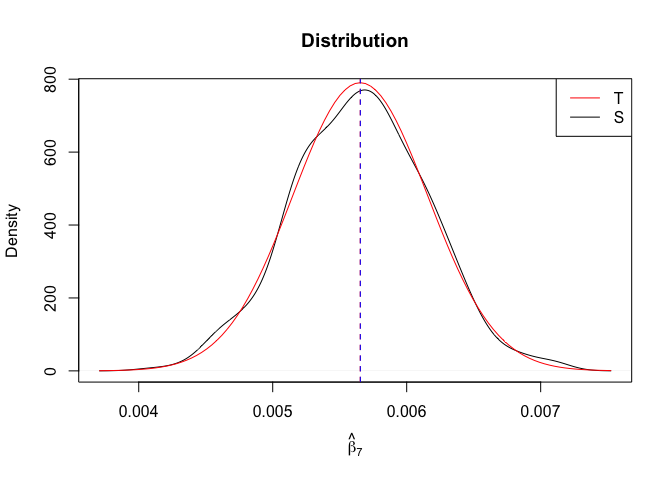
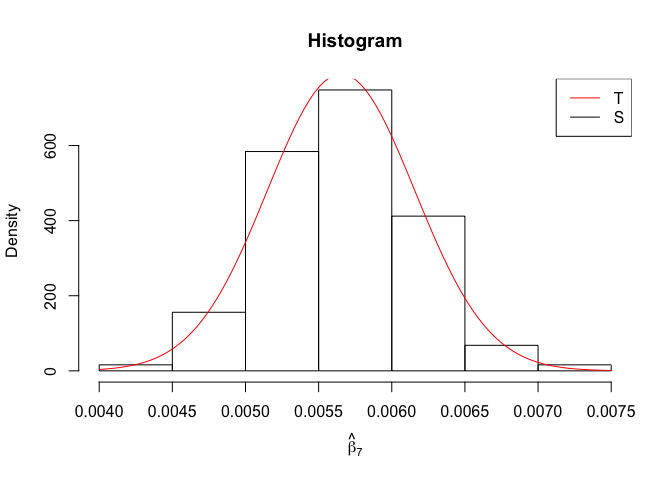
1 | rm(list=ls()) |
Finding (i)
- The O.L.S. estimators of the unknown coefficients and error variance are unbiased
1 | foo = expression(hat(beta)[1], hat(beta)[2],hat(beta)[3],hat(beta)[4],hat(beta)[5],hat(beta)[6],hat(beta)[7]) |
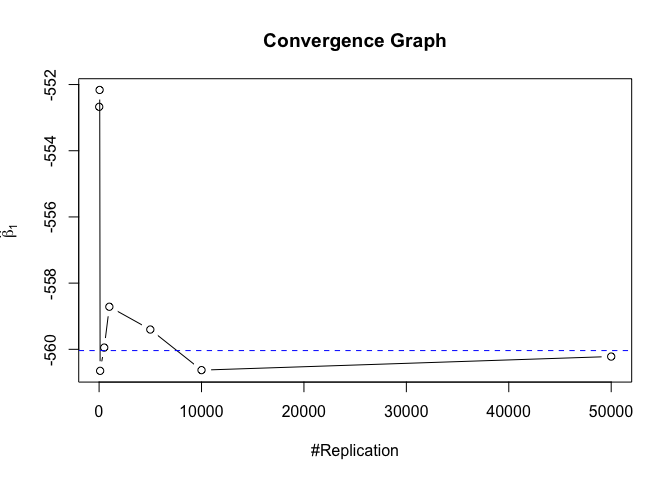
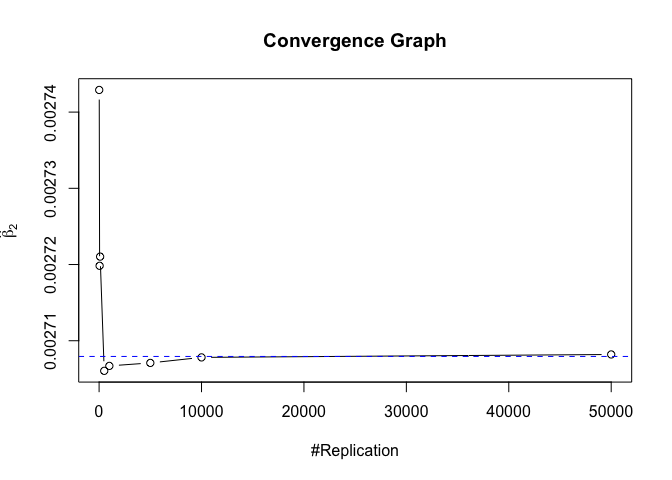
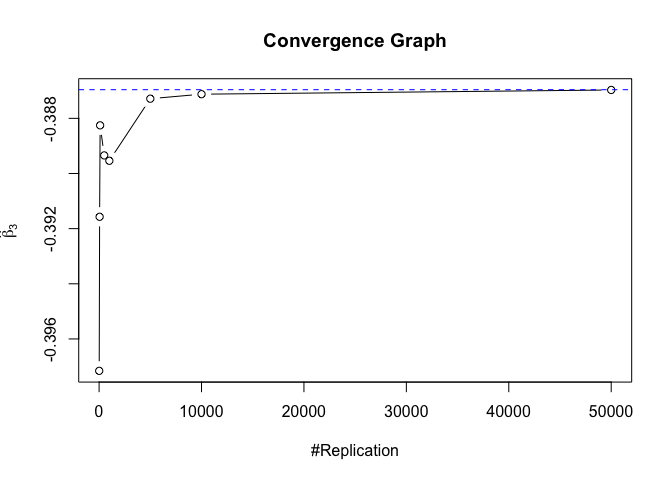
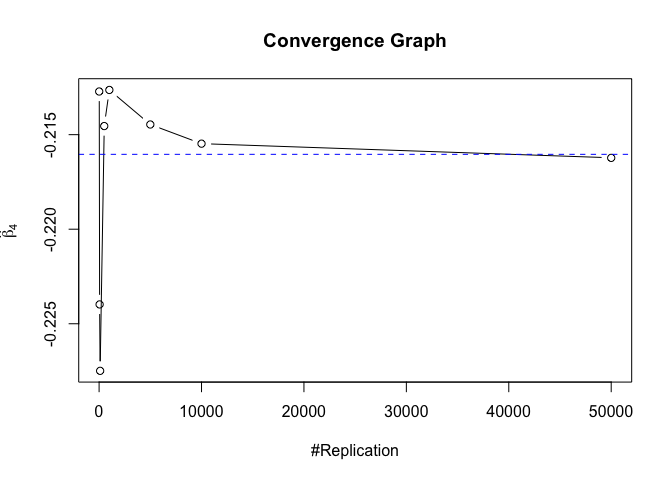
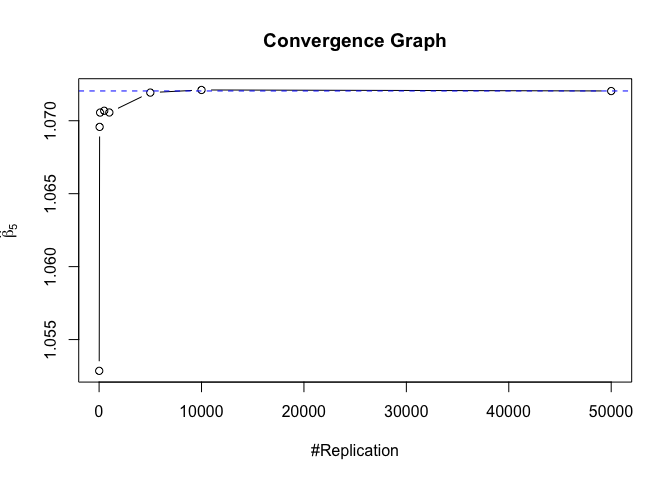
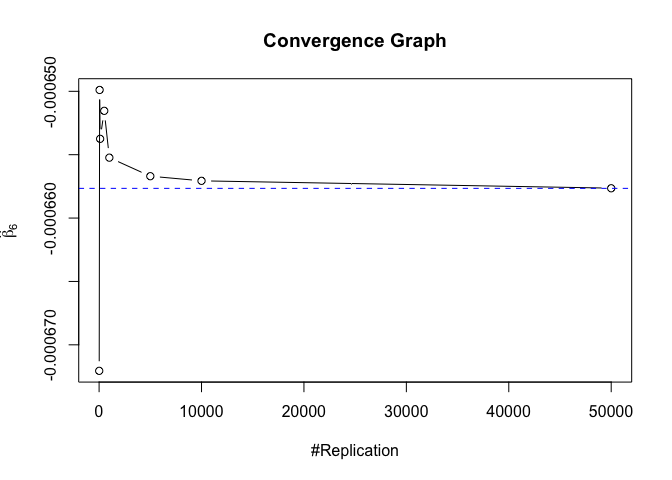
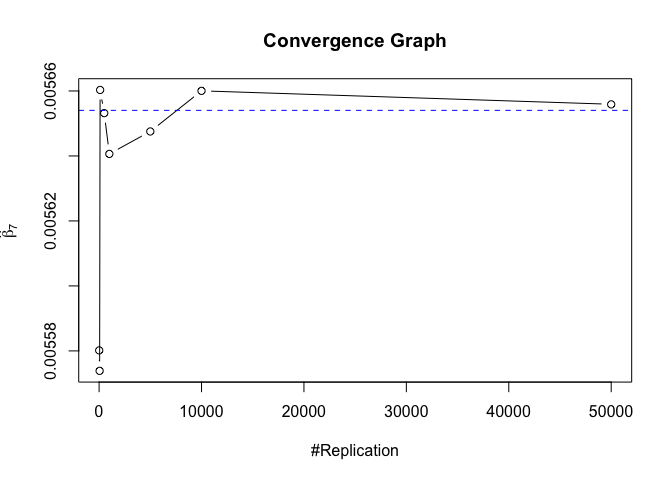
1 | # Error Variance |
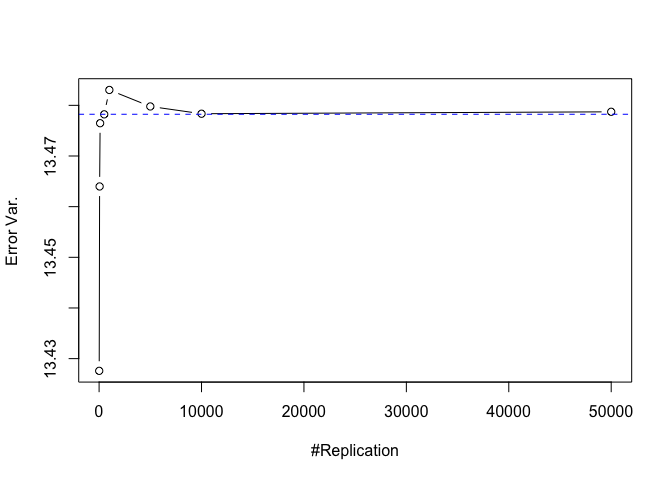
1 | # dev.off() |
Finding (ii)
- The “correct” meaning of a 100(1‐α)% confidence interval of an unknown coefficient
1 | for (i in 1:length(beta)){ |
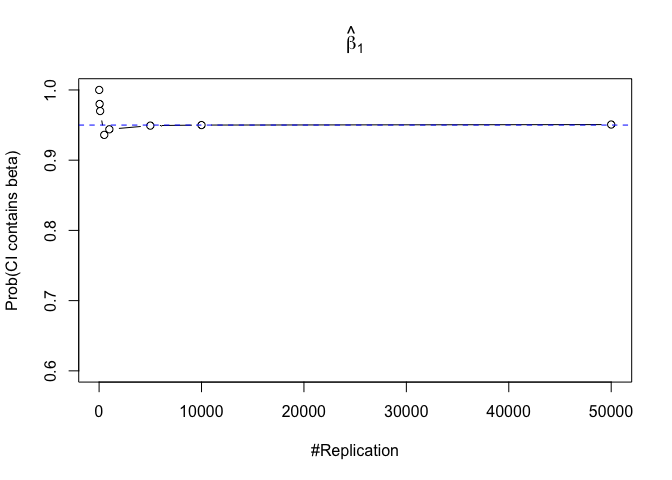
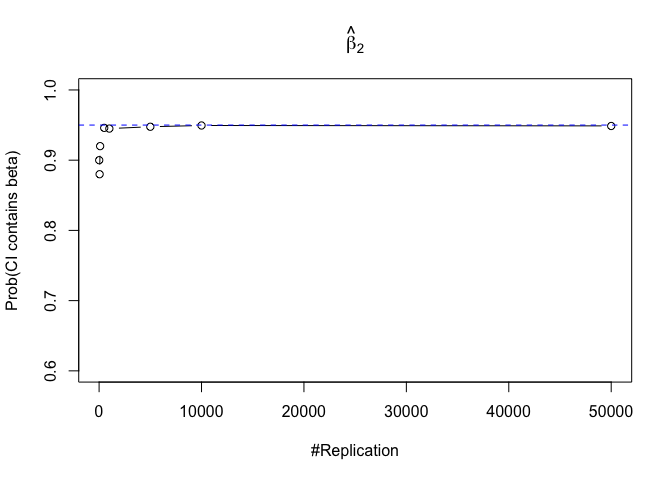
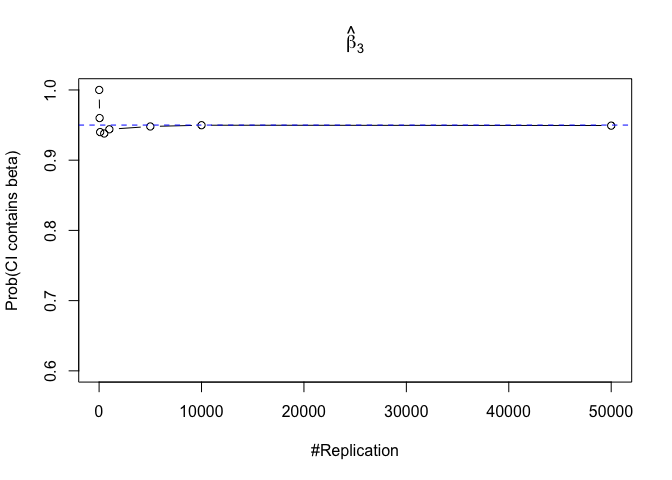
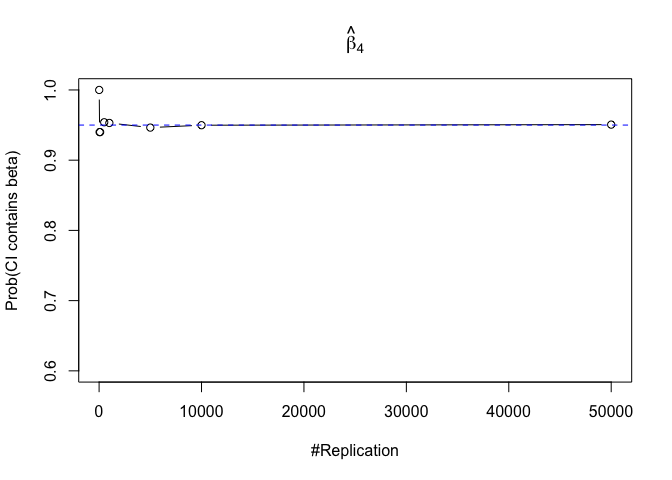
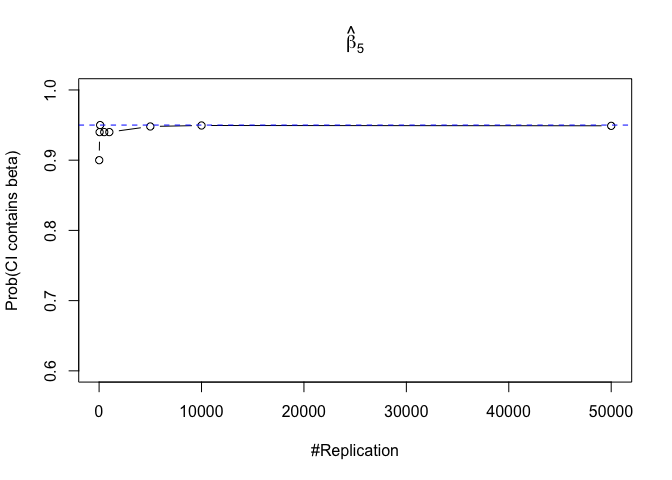
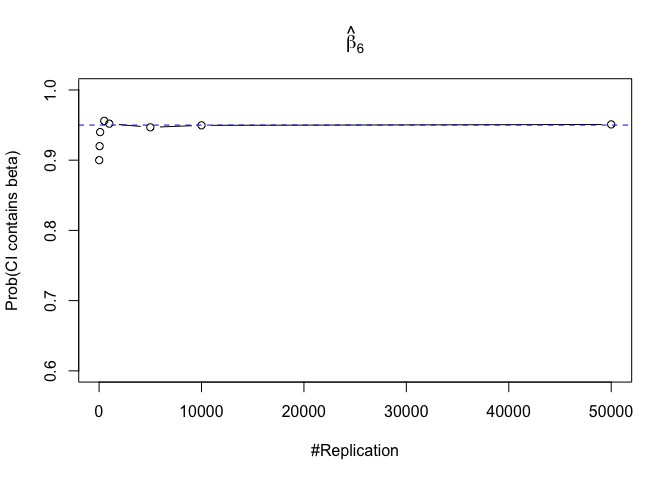
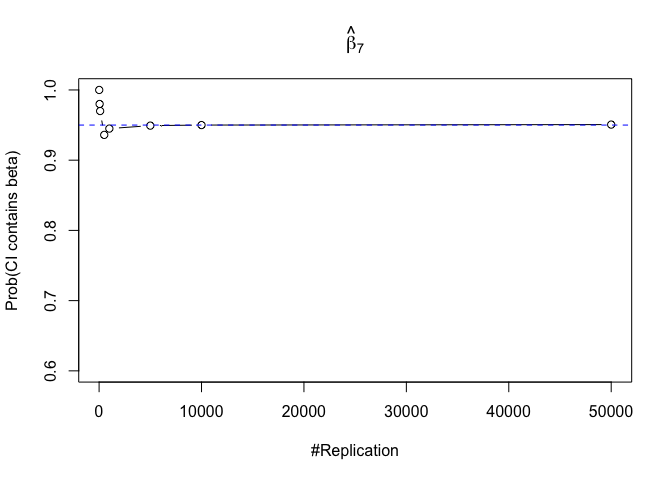
Finding (iii)
- The significance level of the t test for testing a linear hypothesis concerning one or more coefficients is the probability of committing a Type I error
1 | for (i in 1:length(beta)){ |

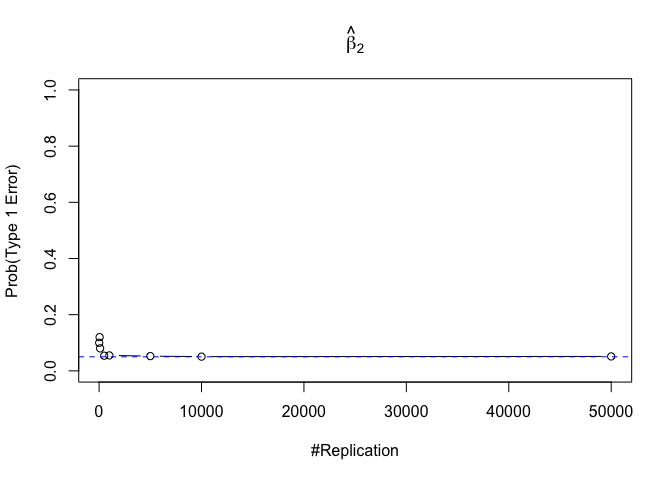
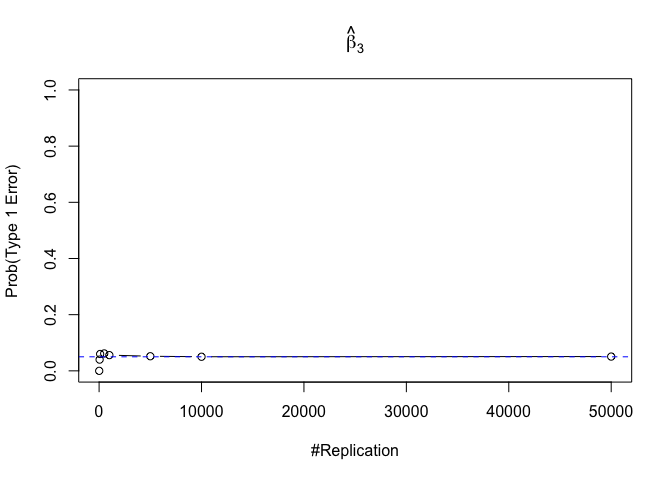
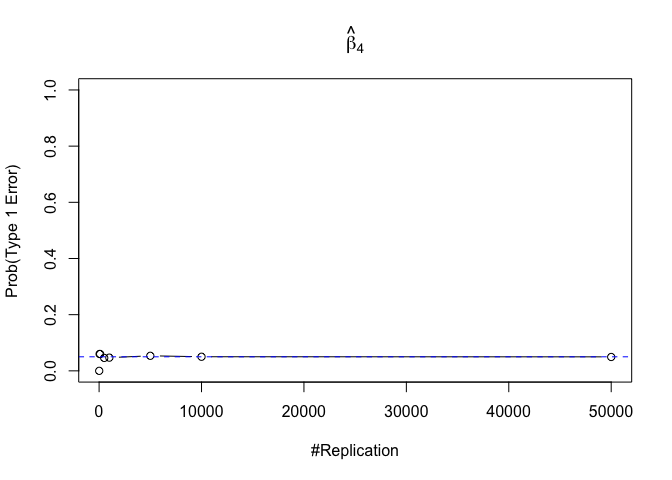
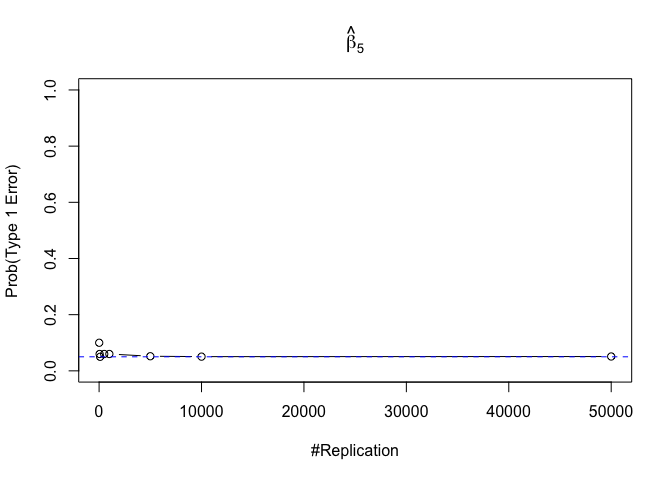
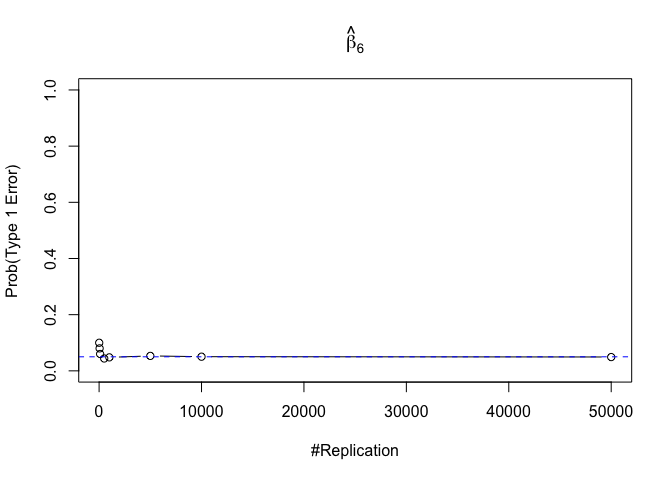
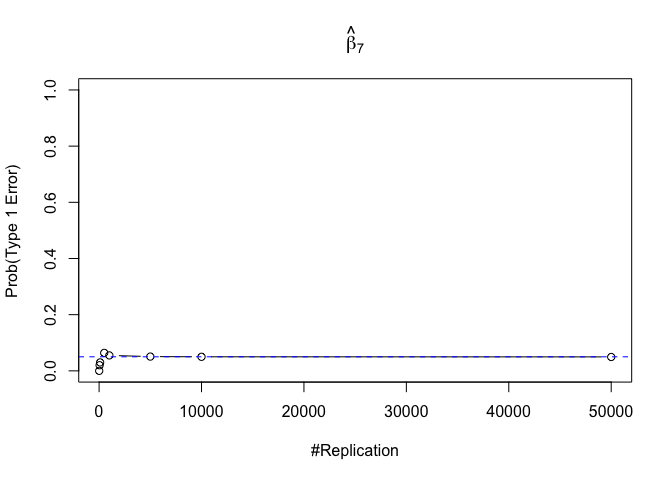
Finding (iv)
- The t test is unbiased
1 | for (i in 1:length(beta)){ |
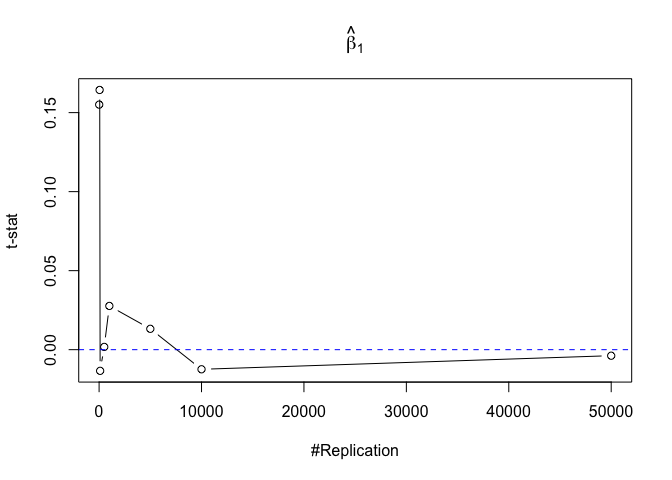
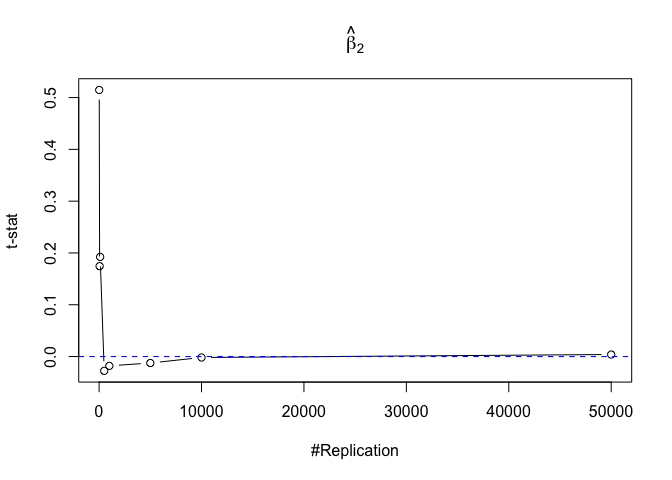
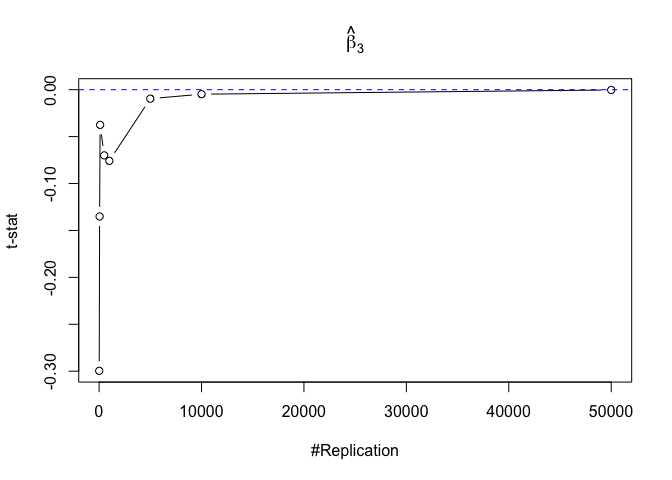
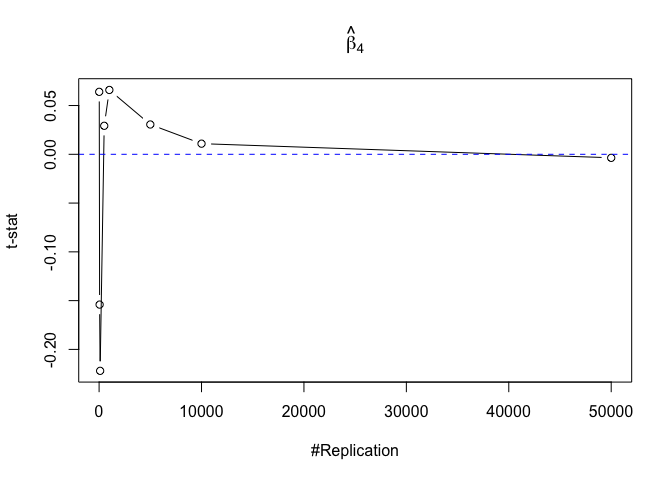
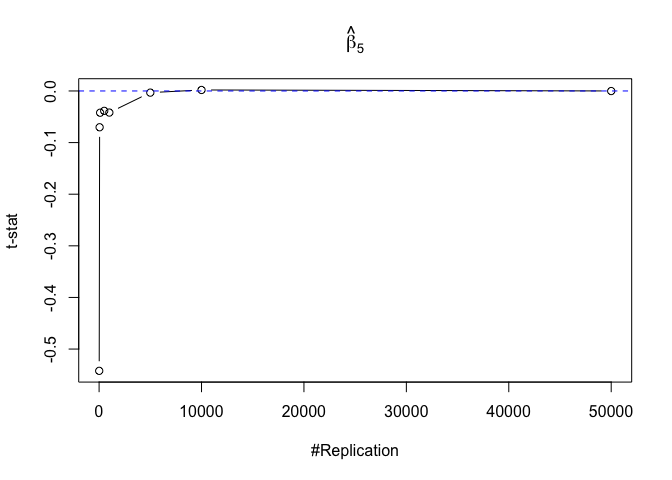
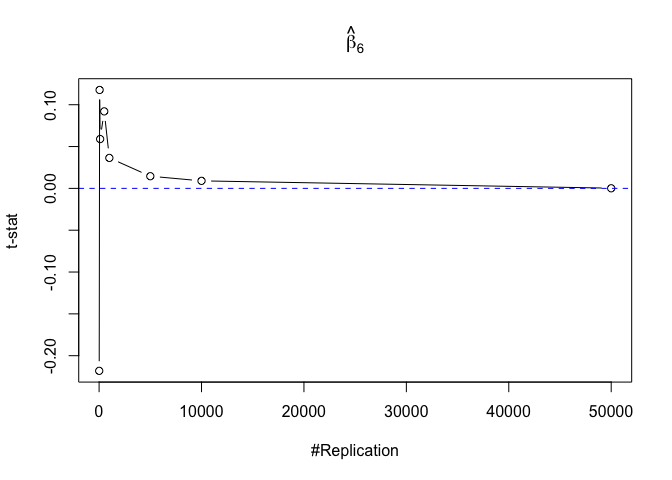
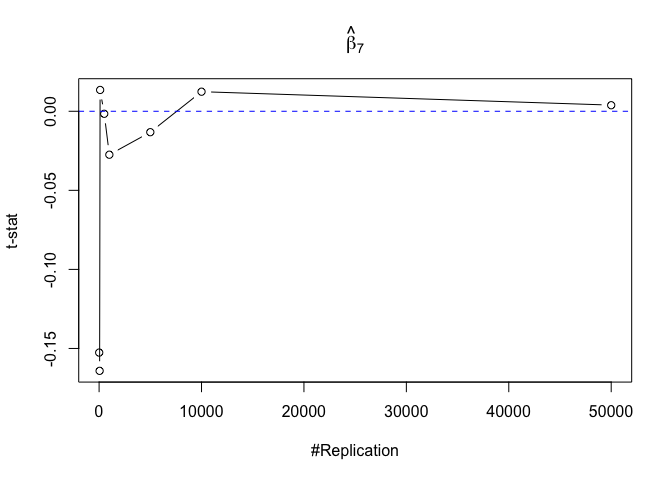
Finding (v)
- The result in Part iii) no longer holds if some relevant explanatory variables have been omitted from the model
1 | foo3 = expression(hat(beta)[12], hat(beta)[22],hat(beta)[42], hat(beta)[52], hat(beta)[62], hat(beta)[72]) |
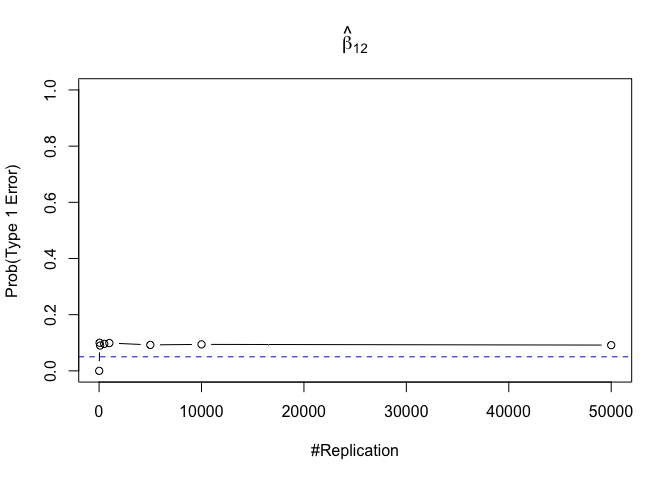
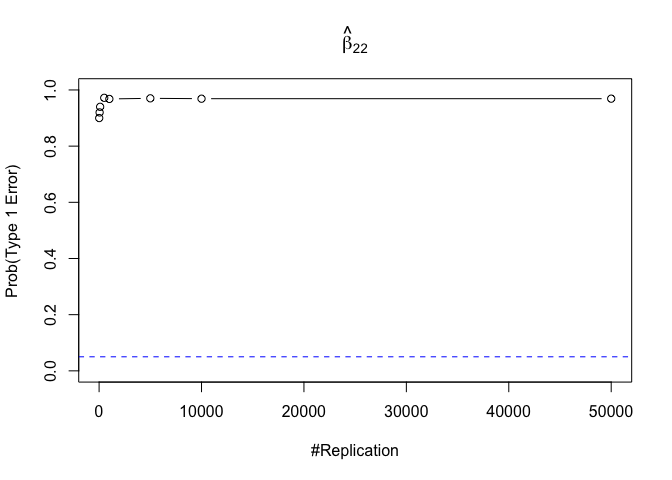
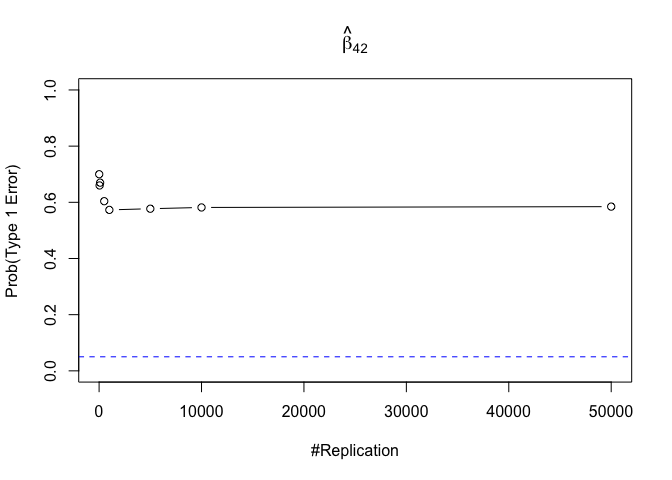
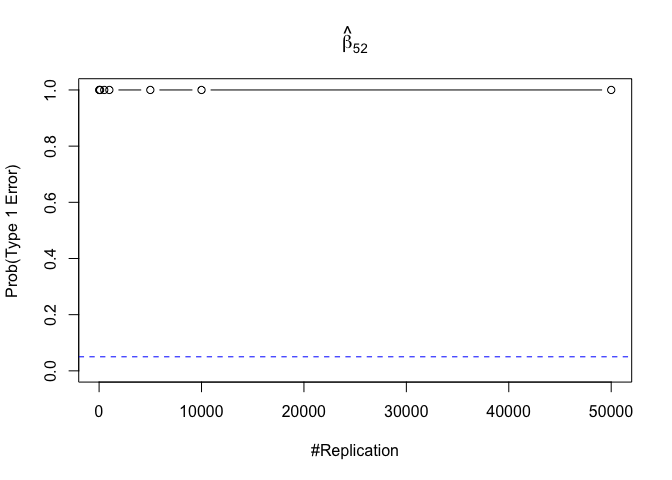
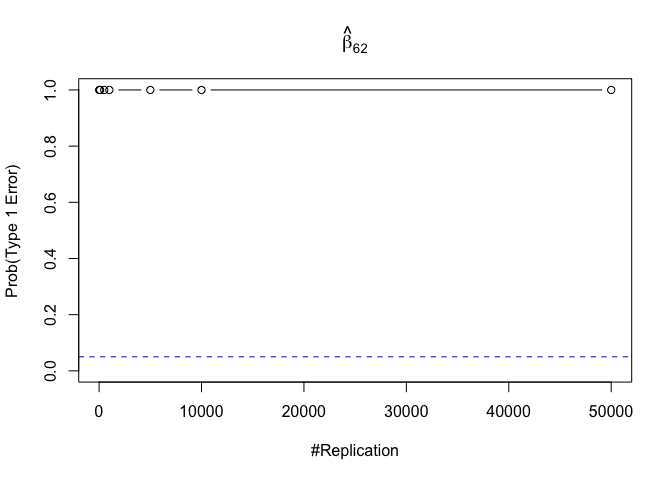
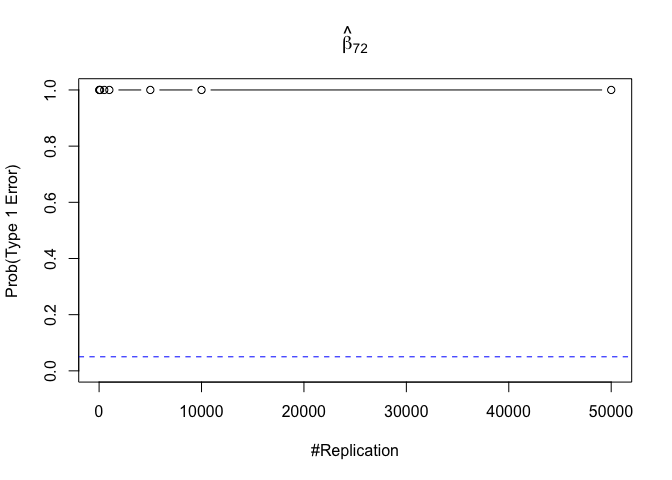
Finding (vi)
- The estimator of say, the coefficient of X2, is no longer unbiased if the decision of whether to include X1 in the model is dependent on the outcome of a t test. Based on your findings, discuss the wider implications of “model selection” for statistical modeling and the lessons to be learnt for practitioners.
1 | nbv = c(1,2,4) |
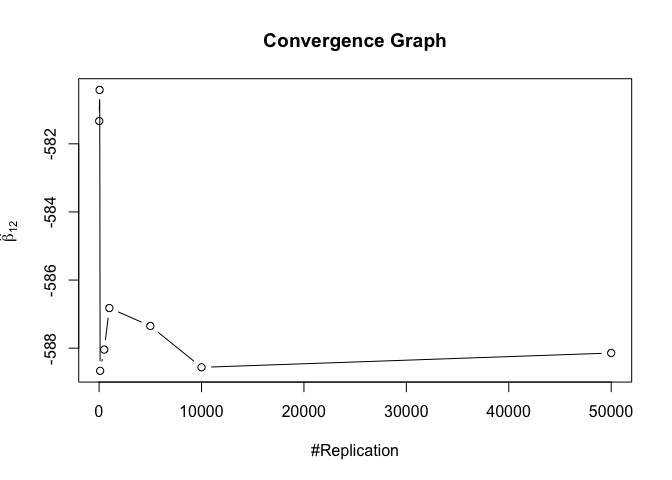
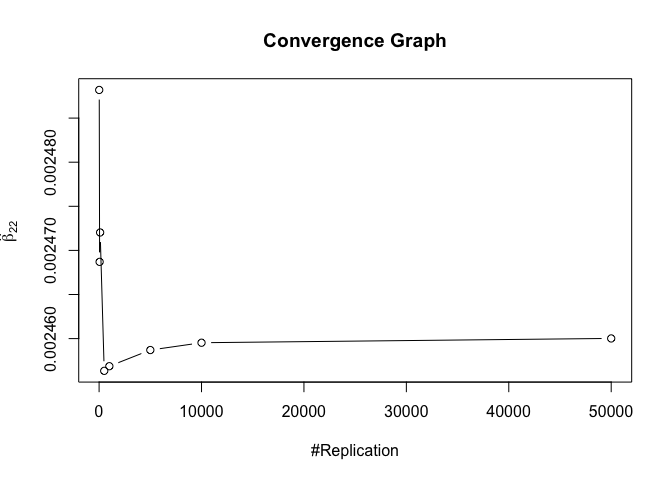
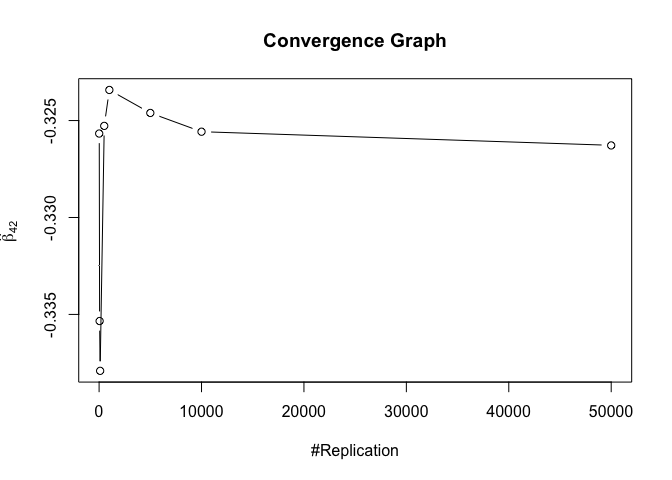
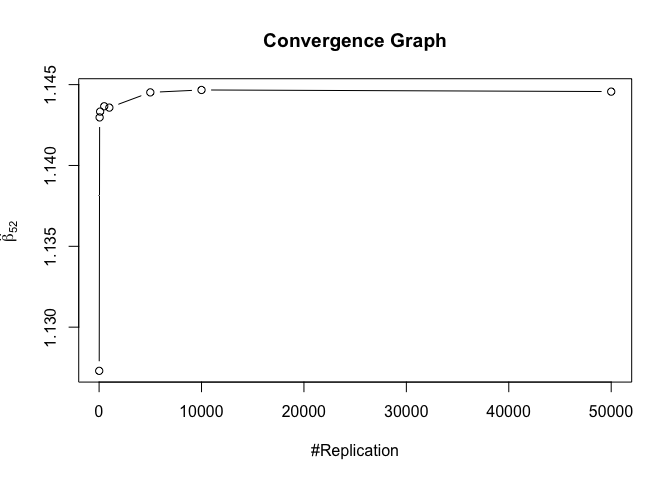
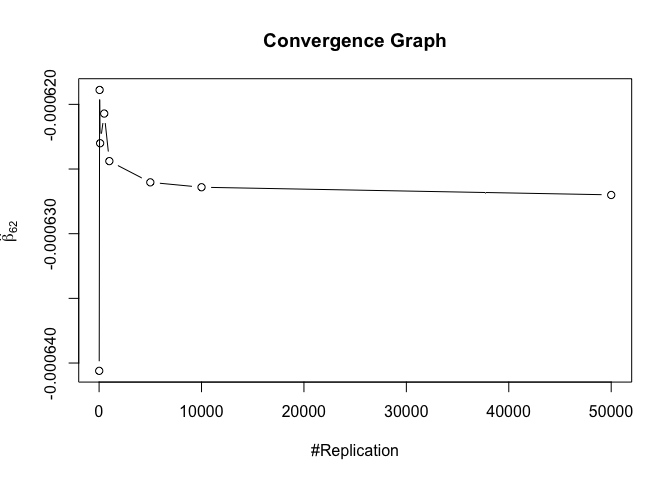
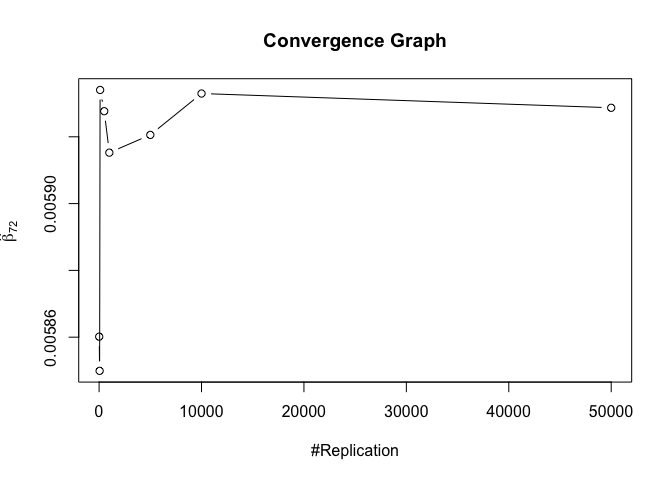
1 | # Error Variance |
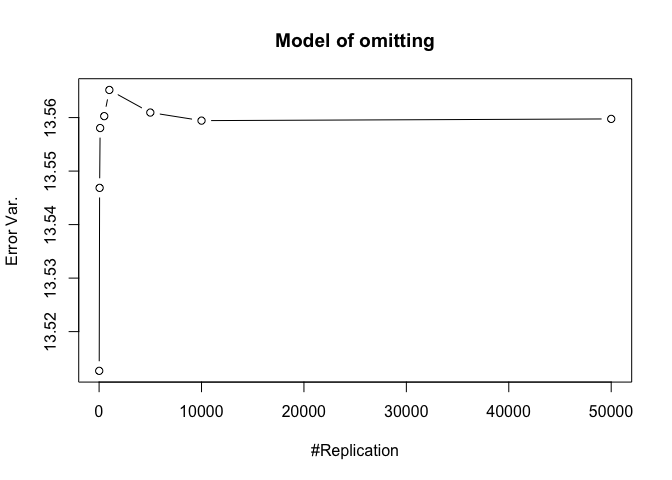
1 | # dev.off() |
